Kimberly Elam的幾何設計理論

 

　　拋出第一個問題：當你不能把它做得更美的時候，問題出在哪裡?我們還有沒有其它辦法突破和超越現有的設計瓶頸呢?

　　讓我們走進神奇的自然界，走進Kimberly Elam的Geometry of Design，去認識那些存在於人與自然界中的基礎規律。松果、鲑魚、人體 有什麼共同的特點?松果、鲑魚、人體，它們都用些什麼共同特點?其實他們都有各種自然比例的規律，這些規律為許多藝術家和設計師的作品，提供了基本的出發點。

　　松果的秘密：松果有8條順時針生長線和13條逆時針生長線，8：13引出一個有趣的比值，那就是1：1.625;這說明了什麼呢?讓我們接著往下看：

　　向日葵與松果一樣，它每顆種子都同時屬於這兩條螺旋線：21條順時針螺旋線，34條逆時針螺旋線，形成的比例是1：1.619，非常接近黃金分割率。

　　由此正式引出我們今天要認識的主角：黃金分割比率以及學習運用它幫助我們從混亂走向秩序。

　　黃金分割是一種數學上的比例關系，它給畫面帶來美感，令人愉悅。在很多藝術品以及大自然中都能找到它。希臘雅典的巴特農神廟，達·芬奇的《維特魯威人》，《蒙娜麗莎》的臉也符合黃金矩形，《最後的晚餐》同樣也應用了該比例布局。

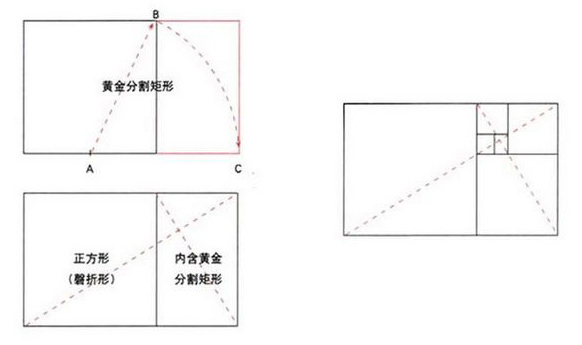
　　由上圖可以簡單理解黃金分割矩形的形成：

　　1.一個正方形邊線的中點A向對角B畫一條斜線，以斜線為半徑畫出的弧線，與正方形的延長線相交於C點。構成一個黃金矩形;

　　2.大矩形和小矩形的對角線和邊線的相交點，成為黃金二次分割的起始線;

　　3.這個分割過程可以無限繼續下去，產生許多更小的等比的矩形和正方形。

　　鲑魚的完美比例：鲑魚的眼睛位於二次黃金分割矩形的水平邊上，尾鳍位於二次黃金分割矩形中;且鲑魚的身體長度正好等於三個黃金分割矩形的長度。

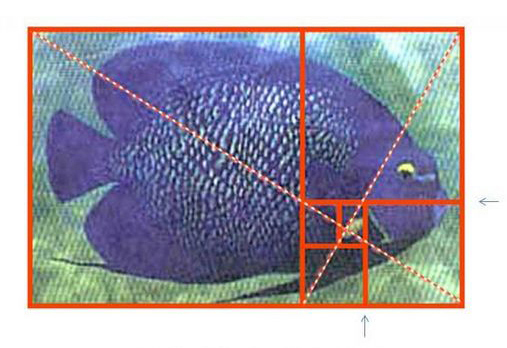
　　天使魚的完美比例：天使魚的身體比例也是完美的黃金分割矩形，其嘴和腮都位於二次黃金分割的矩形上。

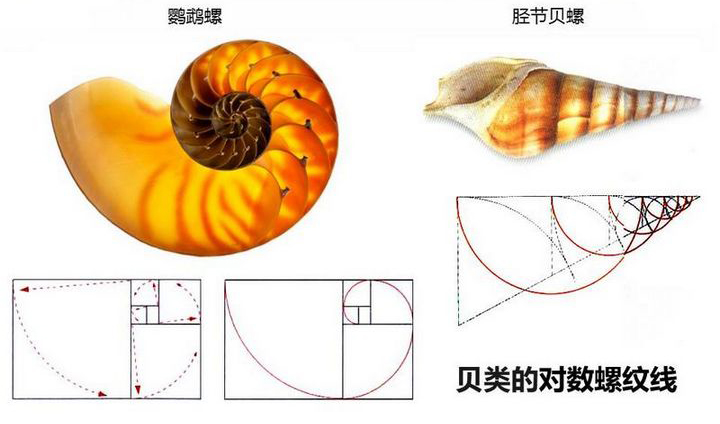
　　貝類的螺旋輪廓線顯示其成長過程的積澱方式是以各種黃金分割比例形成的，對數螺紋線，被認為是完美的成長方式。

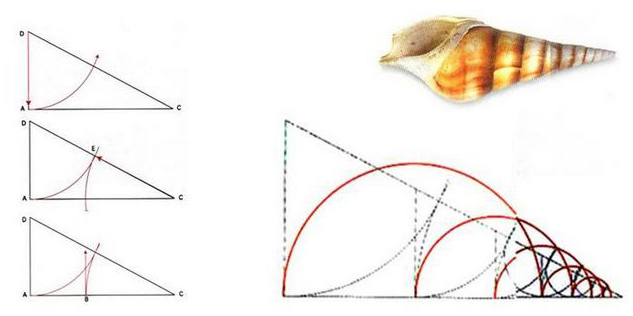
　　從胫節貝螺的生長螺紋線可以看出：

　　黃金分割三角形是它不斷趨向完美生長的方式，每一個節點都是一個輪回的起點，這樣神秘的幾何學生長規律，已經成為許多科學研究與藝術研究的課題。

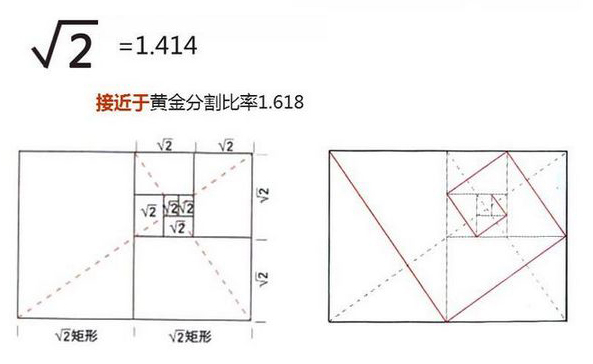
　　√2矩形具有特殊的性質，能被無限分割為 等比 更小的矩形。

　　√2矩形，具有特殊的性質：

　　它能被無限分割為等比、更小的矩形。它接近於黃金分割比例的1.618，

　　√2矩形比例是歐洲DIN紙張尺寸體系的基礎，這個標准體系不僅簡單快捷，它的特殊規律性，在最大限度利用紙張沒有任何浪費。

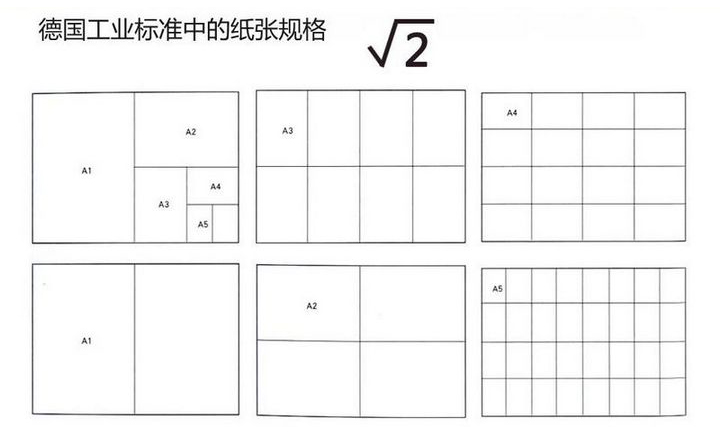
　　這是我們身邊打印室中常見的紙張規格，其實一些看似不相關的數值或比例，都是有規律可尋的，需要我們進一步去認識它們和學會使用它們。

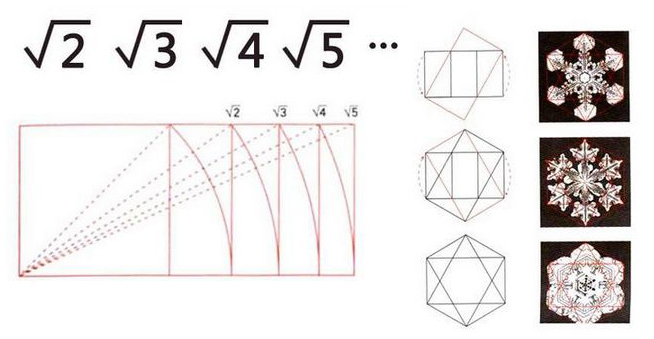
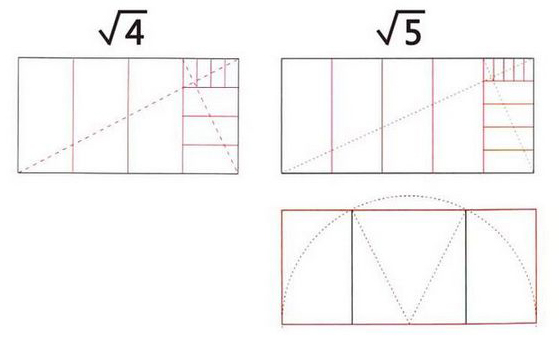
　　√3，√4，√5矩形之間的規律，我們可以由上圖看出：

　　√3矩形是由√2矩形的對角線，作為半徑畫出的弧線相交點的垂直延長線所構成，同理√4，√5也是這樣推導，

　　√3矩形具有構成一個正六稜柱結構的特性，能在雪花晶體的形狀、蜂巢和自然界許多地方找到。

　　在後面的舉例中，我們也能找到這些完美黃金分隔幾何圖形的影子。

　　這裡我們順帶簡單介紹一下斐波那契數列，對於很多設計師來說，可能聽說過但不知道具體個神馬東西?

　　比薩的列奧納多，又稱斐波那契(Leonardo Pisano ,Fibonacci, Leonardo Bigollo，1175年-1250年)，意大利數學家，西方第一個研究斐波那契數，並將現代書寫數和乘數的位值表示法系統引入歐洲。

　　斐波那契數列還有兩個有趣的性質:

　　1.斐波那契數列中任一項的平方數都等於跟它相鄰的前後兩項的乘積加1或減1;

　　2.任取相鄰的四個斐波那契數，中間兩數之積(內積)與兩邊兩數之積(外積)相差1

　　用這個數列解釋兔子繁衍問題，是個比較有趣的過程：感興趣的童鞋可以詳細解一下：http://baike.baidu.com/view/112871.htm

　　接下來我們可以欣賞一下古希臘雕塑中的人體比例規律：

　　人體和許多動植物一樣，也具有黃金分割率，多裡奪弗羅斯和宙斯，它們兩個人的比例幾乎一樣

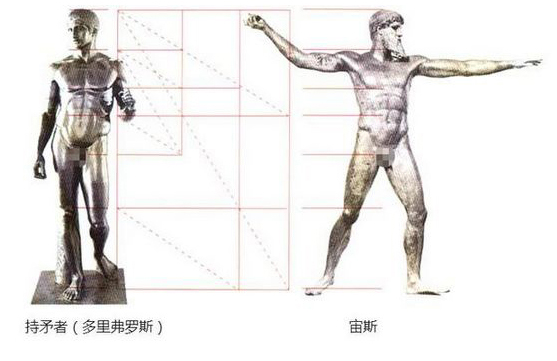
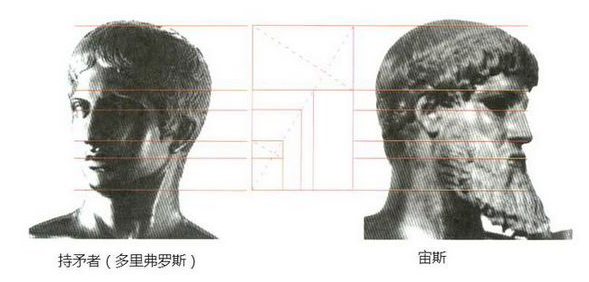
　　同樣，兩者面部的比例幾乎一致：

　　用一個黃金分割矩形來分析頭部的高和寬。

　　這個黃金分割矩形又被更小的黃金分割矩形進一步劃分，以控制面部器官的位置。

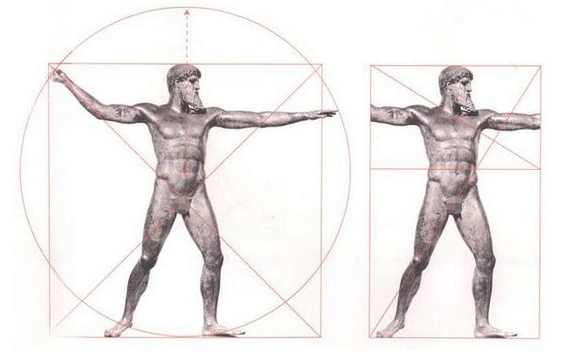
　　一個正方形將宙斯人體圍住，而手和腳正好落在以肚臍為圓心的圓上，其腹股溝處被等分為兩部分，肚臍則位於黃金分割點上。

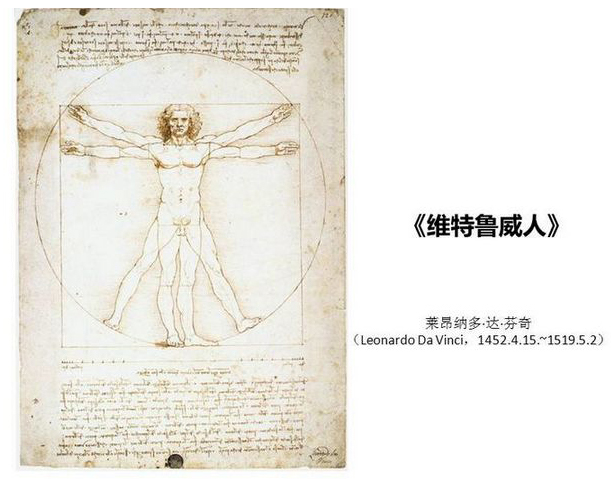
　　由此引出我們熟悉的《維特魯威人》

　　這是一幅達·芬奇依照維特魯威定律所作的鋼筆畫素描，現藏於威尼斯的學院美術館。

　　這幅素描中所畫的男子形象被世界公認為是最完美的人體黃金比例。