MAYA粒子制作動態龍卷風

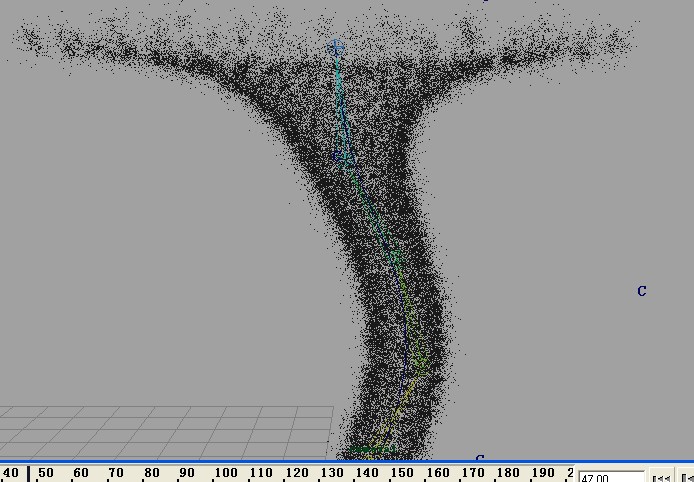
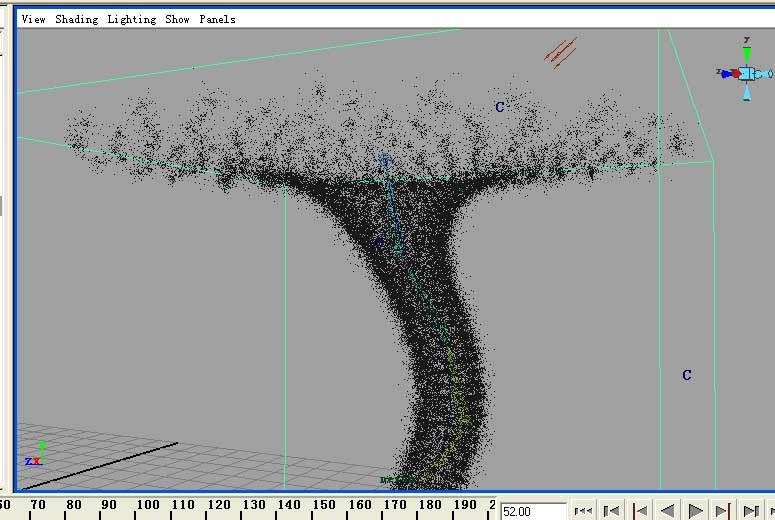
　　因為需要，查看了些資料，制作了動態的龍卷風，先看效果。

　　首先畫一條曲線，不要分太多的段，對其進行從建，如下圖。作用會在下面講到。並將曲線改名為axis

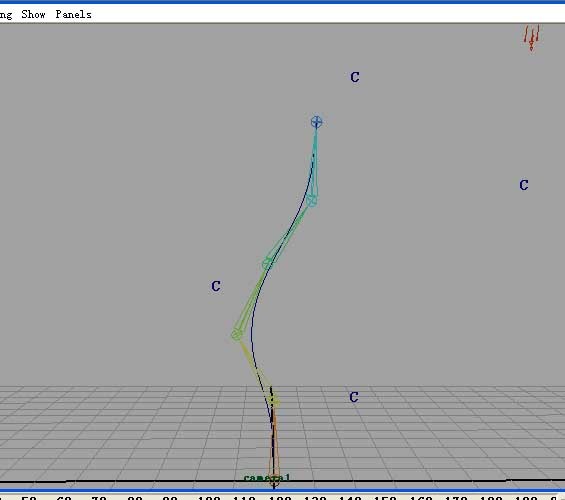
　　制作一段骨骼，並給骨骼一個線條IK，將曲線綁定到骨骼上.利用骨骼運動帶動曲線運動.大家可以用簇變形來做，怎麼做大家都會吧.要將每個蔟子化到梗骨骼上，方便整體運動.如圖

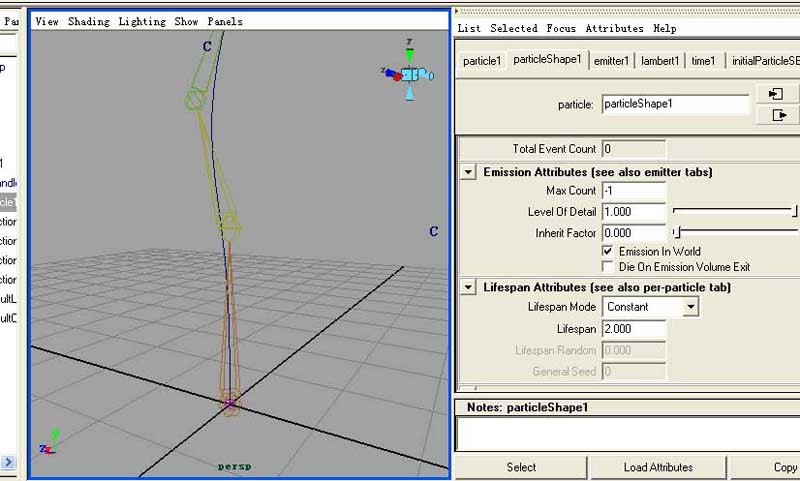
　　下面，關鍵時刻到了.建立一個粒子發射器.簡單的進行設置，如圖

　　現在給粒子的位置屬性設置表達式：

　　float $para=sin(1.57*particleShape1.age/particleShape1.lifespan);

　　float $poi[]=`pointOnCurve -pr $para -p axis`;

　　float $rad=0.6+pow(particleShape1.age/1.5,6);

　　float $ang=particleShape1.age*3+(particleShape1.particleId+rand(0.1,0.3))*0.25;

　　float $x=$rad*sin($ang);

　　float $z=$rad*cos($ang);

　　particleShape1.position=<<($x+$poi[0]),$poi[1],($z+$poi[2])>>;

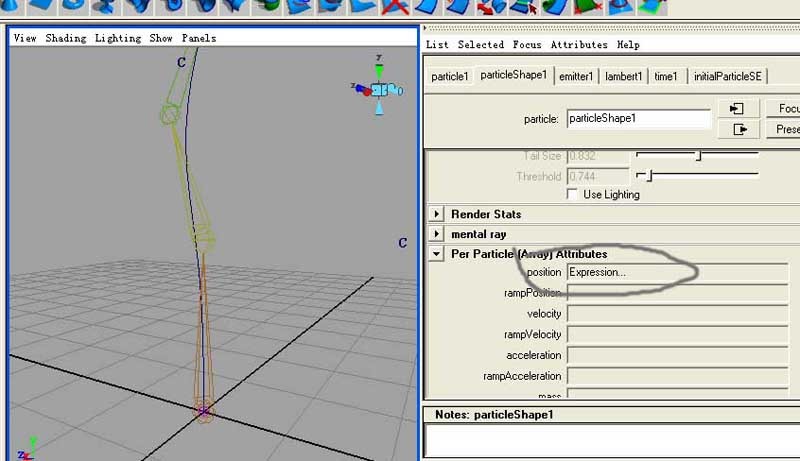
　　然後對梗骨骼的位移進行動畫，龍卷風就會跑起來.下面，我來對表達式進行解釋.

　　float $para=sin(1.57*particleShape1.age/particleShape1.lifespan);

　　這句大家可以發現"particleShape1.age/particleShape1.lifespan"，particleShape1.age的值是從0到particleShape1.lifespan，而particleShape1.lifespan的值始終是2，不變，所以"particleShape1.age/particleShape1.lifespan"的值就是從0到1，而1.57是弧度值對應的角度值是90度.所以

　　"$para=sin(1.57*particleShape1.age/particleShape1.lifespan)"的值就是從0到1，這是粒子中常用的技巧.而第2句float $poi[]=`pointOnCurve -pr $para -p axis`利用到了$para，我來解釋下這句，pointOnCurve是個獲得曲線信息的命令　-pr是曲線參數命令，後面跟的是個數　，而$para的范圍正好覆蓋了整個曲線，0-1

　　(因為重建曲線時已經標總化，大家可以回頭看看)　-p 　得到的是每個點的空間坐標，是個失量，axis是曲線名，必須跟在後面.然後將得到的每個點的空間位置存在一個數組$poi[]中.記住加單引號，是ESC鍵下面那個，別搞錯了.

　　這樣就找到了曲線上每點的空間位置信息.float $x=$rad*sin($ang);

　　float $z=$rad*cos($ang);這兩句比較好理解，是圓周運動必要的.前面的$rad是半徑.float $rad=0.6+pow(particleShape1.age/1.5,6);用一個函數定義了半徑的變化，也就是龍卷風從下到上的半徑變化.為什麼用這麼一個函數呢?因為他的曲線符合我的要求，你們也可以用別的函數來定義.

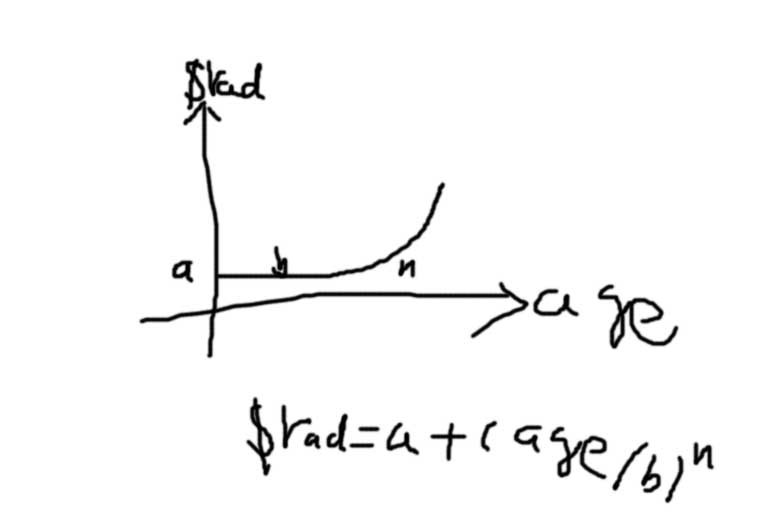
　　a越大，龍卷風的半徑越大，b越大轉彎處離根部越

　　遠，N越大則轉彎越急.

　　float $ang=particleShape1.age*3+(particleShape1.particleId+rand(0.1,0.3))*0.25;

　　這句很明顯，particleShape1.age*3是讓粒子持續運動，(particleShape1.particleId+rand(0.1,0.3))*0.25;是讓每個粒子的初始轉角不同，這樣才會行成面，不會是線.particleShape1.particleId大家都知道吧，每個粒子的都不同.

　　particleShape1.position=<<($x+$poi[0]),$poi[1],($z+$poi[2])>>; 最後將粒子自身定義的運動與曲線上點的位置疊加就可以了.我只是給大家一個思路，大家自己回理解的.

        注：更多精彩教程請關注三聯圖文教程 頻道，